A引入

当然，这只是一个大学生PID的学习笔记

A.1什么是PID

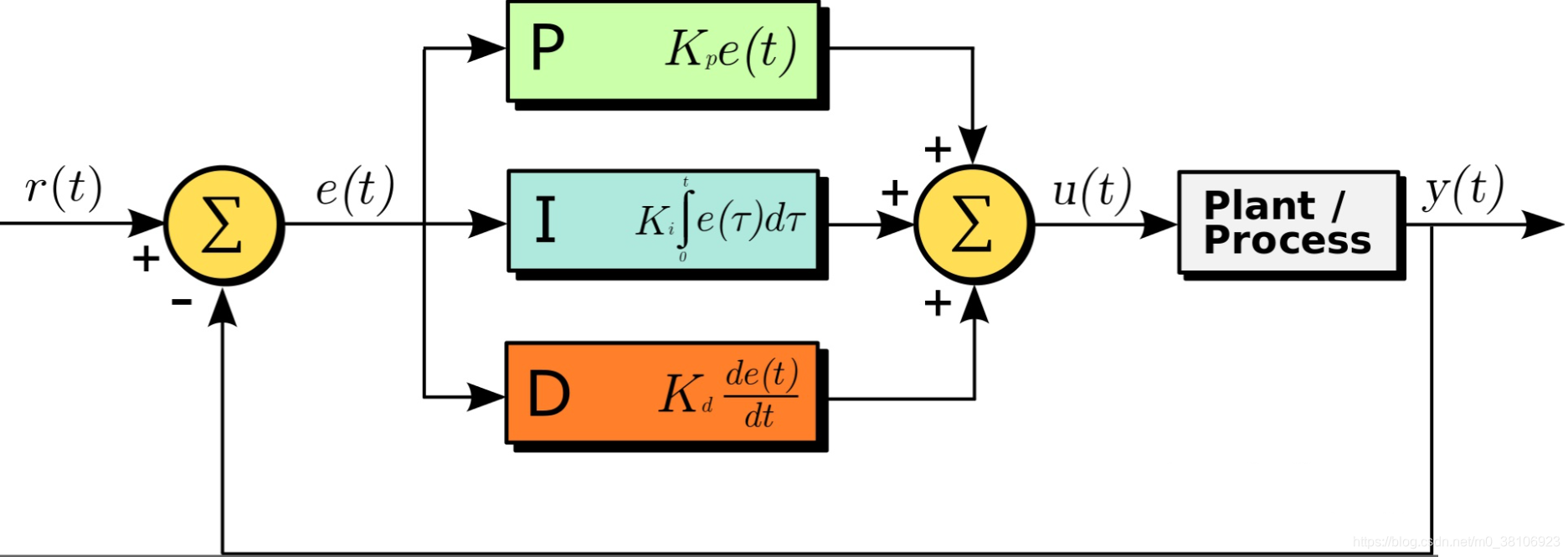
PID，就是“比例（proportional）、积分（integral）、微分（derivative）”，是一种常见的控制算法，可以用在平衡小车，温度控制等场所，用于让一个物理量“保持”稳定（转速，温度，速度等）。

A.1.1比例环节（kp）

假如现在要控制水温，我们期望它达到的温度为目标值，它当前的温度为当前值。如果现在当前值低于目标值，那么我们可以加热（增加功率），当当前值高于目标值，那我们可以减少功率（散热）。这个时候会有几种情况

当前值和目标值差距很大，那我们需要开大火加热
当前值和目标值差距适中，那我们需要开中火大热
当前值和目标值差距很小，那我们只需用轻轻加热
而比例环节便是控制火应该开多大开多小，我们会发现开火的的大小和目标值与当前值的差值（温差）有关，我们把这个差值记作偏差，用kp与偏差建立一个一次函数关系便可以控制这个加热功率的大小

输出 = kp偏差
#kp是一个系数，具体需要自己根据实际调节，下面的kd，ki与此相同
#这里和下面的输出泛指对被控对象的*调节力度

但是光一个比例环节并无法很好的控制水温，温度还是会在目标值周围变化，因为当你达到目标值的时候，温度还在增加，温度的（变化速率）在这个过程中并没有趋近于0，所以还需要有一个环节来让它趋于0，起到一个阻尼的作用，这个环节便是微分环节。而我们最常用的PD控制器，就是由这两个环节共同构成。

A.1.2微分环节（kd）

在比例环节中的热水例子中，我们发现水温的变化速率没有办法趋于0，所以发明pid算法的人就研究了一个方法：当当前值与目标值接近的时候，比例环节（P）的控制作用变得很小，而微分环节（D）作用是让物理量的速度趋于0，如果升温速度很大，那么它就施加一个反方向的“力”，让降温速度增加，反之让升温速度增加。

输出 = kd*偏差的微分
#距离的微分就是速度
#温差的微分就是温度变化速度
#离散状态下的微分计算就是把这一轮计算得到的误差与上一轮的误差相减

这个时候，我们的水温看似已经可以稳定在目标值了，在没有外界干扰或其它情况下确实可以，但是出现下面的情况：
干扰条件:天气很冷，使得散热的速度与加热的速度基本相等了。
假设目标温度是50摄氏度，但是当到了48摄氏度的时候，比例环节（P）发现温差很小，对功率的控制力很小，轻轻加热即可，这个时候，如果升温速度和降温速度也很接近，那么微分环节（D）便会罢工，什么都不干，那么温度便会一直停留在48摄氏度，但是我们的目标值却不是它。这个时候我们应该继续加热才可以达到目标温度，而这个实现的步骤便是积分环节（I），这个一直存在的误差，我们称为稳态误差。

A.1.3积分环节（ki）

积分环节的作用就是当误差存在时候，发挥作用让值往目标值移动。
设置一个积分值，当误差存在的时候，就对它积分（在离散数据下就是累加），并且让这个积分值作用到调节力度上
在加热这个例子上，当水温一直停留在48摄氏度的时候，误差仍旧存在，一直是2，那么这个积分值便会一直一直累加，并且反馈到调节力度（加热）上，当水温重新加热到目标值附近，这个积分值不再累加，此时的加热与散热再次持平，那么水温便达到我们预期的目标值了，可喜可贺。

输出 = ki*偏差的积分
#通常我们测量的都是离散的数据，那么温差的积分就是温差值不断累加

最后我们讲得到的三个值相加，便是我们最终需要给被控度对象施加的调节力度了。

A1.4PID过程常用的专业术语

被控对象：需要控制的对象，案例中指水
目标值：期望被控对象达到的状态量，案例中指水的目标温度
反馈值：被控对象当前时刻的状态量，案例中指水的实时温度
输出量：PID的计算结果，案例中指对水温的调节
误差：目标值-反馈值
稳态误差：系统稳定状态下仍存在的误差，如案例中当存在天气很冷的干扰条件时，温度停在了48摄氏度，仍存在误差

阶跃输入：在稳定状态下目标值发生突然变化
阶跃响应：阶跃输入后被控对象的跟随状态，能够代表系统的控制性能
响应速度：阶跃输入后被控对象再次到达目标值的速度
超调量：阶跃输入后，被控对象到达目标值后超出目标值的距离

当然后面这四个量需要看图理解，我参考的这个文章学习的
比例环节：起主要控制作用，使反馈量向目标值靠拢，但可能导致振荡
积分环节：消除稳态误差，但会增加超调量
微分环节：产生阻尼效果，抑制振荡和超调，但会降低响应速度

A1.5积分限幅和输出限幅

我们一般还会对PID的积分和输出进行限幅（规定上下限），积分限幅可以减小积分引起的超调，输出限幅可以保护执行机构或被控对象。

A.2单级PID的写法

先挂一张网上的PID流程图: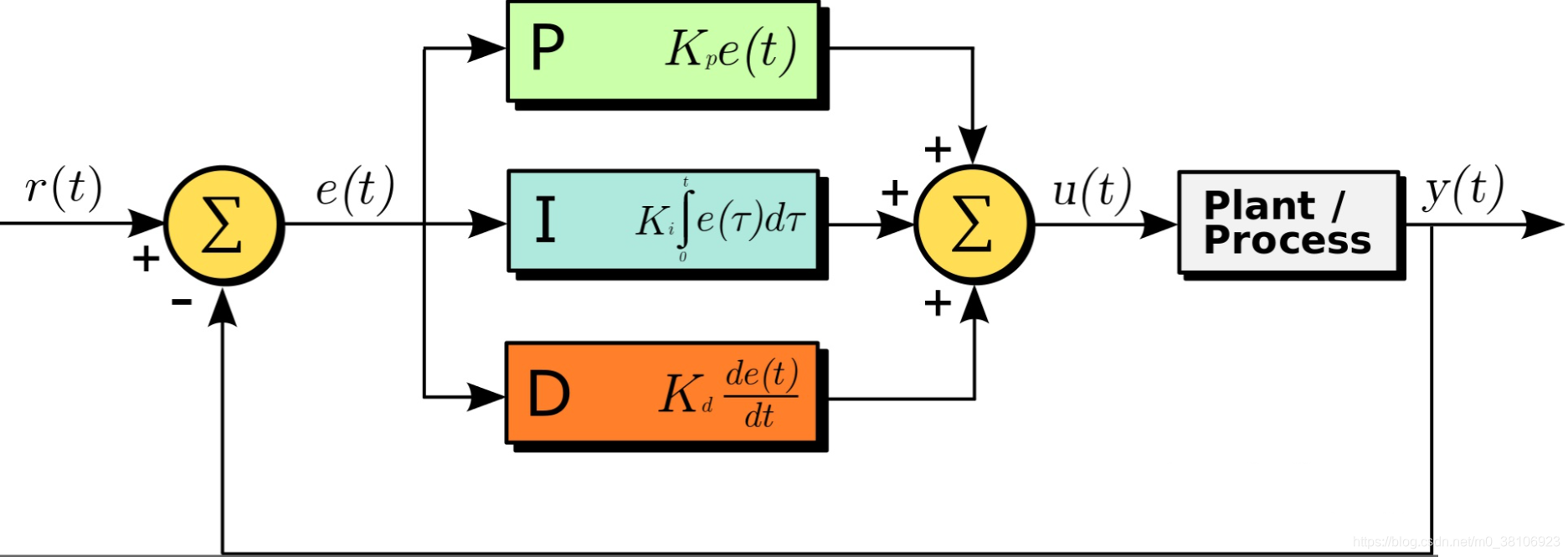

函数流程图: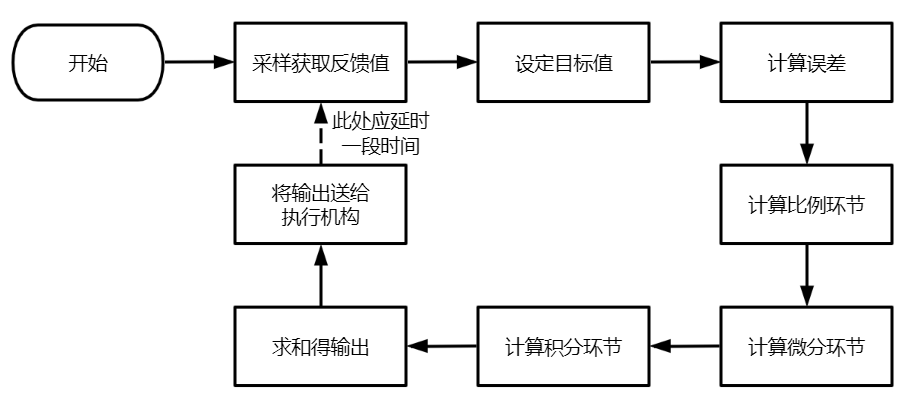

定义PID的参数的结构体

typedef struct
{
  float kp, ki, kd; //三个系数
  float error, lastError; //误差,上次误差
  float integral, maxIntegral; //积分,积分限幅
  float output, maxOutput; //输出,输出限幅
}PID;

初始化PID的参数

void PID_Init(PID *pid, float p, float i, float d, float max_in, float max_out)
{
    pid->kp = p;
    pid->ki = i;
    pid->kd = d;
    pid->maxIntegral = max_in;
    pid->maxOutput = max_out;
}

进行一次PID计算

//参数为：pid结构体，目标值，反馈值
void PID_Calc(PID *pid, float reference, float feedback)
{
    pid->lastError = pid->error; //将旧error存起来
    pid->error = reference - feedback; //计算新error
    //微分环节
    float dout = (pid->error - pid->lastError) * pid->kd;
    //比例环节
    float pout = pid->error * pid->kp;
    //积分环节
    pid->integral += pid->error * pid->ki;
    //积分限幅
    if(pid->integral > pid->maxIntegral) pid->integral = pid->maxIntegral;
    else if(pid->integral < -pid->maxIntegral) pid->integral = -pid->maxIntegral;
    //计算输出
    pid->output = pout+dout + pid->integral;
    //输出限幅
    if(pid->output > pid->maxOutput) pid->output =   pid->maxOutput;
    else if(pid->output < -pid->maxOutput) pid->output = -pid->maxOutput;
}

主函数

PID mypid = {0};//初始化一个PID结构体变量
int main()
{
    //...这里有些其它的初始化代码
    PID_Init(&mypid, 10, 1, 5, 800, 1000); //初始化PID参数
    while(1)//进入循环运行
    {
        float feedbackValue = ...; //这里获取被控对象的反馈值
        float targetValue = ...; //这里获取目标值
        PID_Calc(&mypid, targetValue, feedbackValue); //进行PID计算，结果在output成员变量中
        //...这里写被控对象的执行函数(参数是mypid.output)
        delay(10); //等待一定时间再开始下一次循环
    }
}

当然，在后面具体写平衡小车代码的时候，肯定会有一部分修改，因为更改成串级PID。

A.3从单级PID到串级PID

单级PID是目标值和反馈值经过一次PID计算就得到输出值并直接作为控制量，但如果目标物理量和输出物理量之间不止差了一阶的话，中间阶次的物理量我们是无法控制的。
可能烧水时温度会上升的一会快一会慢，下面用更容易理解的小球举例：

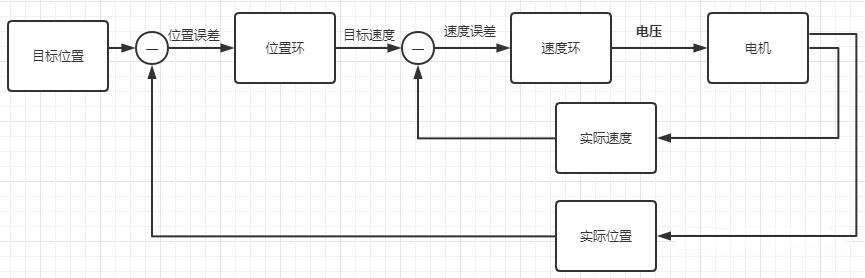
比如：当你要在一个x坐标轴上控制一个小球移动到目标位置。你的目标值是目标位置，反馈值是当前位置，你的输出物理量是加速度，因为是用力来控制小球的（F=ma），而位置与加速度中间还有一个速度值是无法控制的，这会使得小球在从当前位置运动到目标值的过程中不够平稳，而串级PID就是用来改善这一点的

图中的外环和内环就分别是一个单级PID，每个单级PID都需要获取一个目标值和一个反馈值，然后产生一个输出值。
串级PID中两个环相“串”的方式就是将外环的输出作为内环的目标值。
在小球模型中：

可用条件：小球实时位置、小球实时速度、施加在小球上的控制力
目标值：小球目标位置
外环反馈：小球实时位置
内环反馈：小球实时速度
输出值：施加在小球上的控制力

外环获得位置反馈，输出速度作为内环的目标值，内环获得速度反馈，输出控制力的大小控制小球，小球再反馈速度和位置给内环外环，实现小球的稳定运动。

函数部分:

//此处插入单级PID相关代码

//串级PID的结构体，包含两个单级PID
typedef struct
{
    PID inner; //内环
    PID outer; //外环
    float output; //串级输出，等于inner.output，内环输出控制被控对象
}CascadePID;
 
//串级PID的计算函数
//参数(PID结构体,外环目标值,外环反馈值,内环反馈值)
void PID_CascadeCalc(CascadePID *pid, float outerRef, float outerFdb, float innerFdb)
{
    PID_Calc(&pid->outer, outerRef, outerFdb); //计算外环
    PID_Calc(&pid->inner, pid->outer.output, innerFdb); //计算内环，外环的输出就是内环的目标值
    pid->output = pid->inner.output; //内环输出就是串级PID的输出
}
 
CascadePID mypid = {0}; //创建串级PID结构体变量
 
int main()
{
    //...其他初始化代码
    PID_Init(&mypid.inner, 10, 0, 0, 0, 1000); //初始化内环参数
    PID_Init(&mypid.outer, 5, 0, 5, 0, 100); //初始化外环参数
    while(1) //进入循环运行
    {
        float outerTarget = ...; //获取外环目标值
        float outerFeedback = ...; //获取外环反馈值
        float innerFeedback = ...; //获取内环反馈值
        PID_CascadeCalc(&mypid, outerTarget, outerFeedback, innerFeedback); //进行PID计算
        //...这里写被控对象的执行函数(参数是mypid.output)
        delay(10); //延时一段时间
    }
}

A.4对PID三个参数的调参环节

在完成代码编写后，最重要的就是调参环节（调节kp，ki，kd）：
通常还是使用经验法调参，通俗而言就是“试参数”，测试多个参数选取最好的控制效果，一般的步骤如下：

单级PID调参：

先将所有参数置零
将输出限幅设为执行机构能接受的最大值
增大p参数，使响应速度达到比较好的水平
若存在稳态误差，逐渐增加i参数和积分限幅，使稳态误差消失
若希望减少超调或振荡，逐渐增加d参数，在保证响应速度的前提下尽可能降低超调

串级PID调参：
一般先断开外环，手动设定内环的目标值，然后同单级pid调节过程，等内环稳定了，然后连接外环继续调参，直到整体都稳定为止。

B应用

当然，这只是一个大学生无聊所想做的，其实也是更实际了解学习一下这个算法的调参啥的

B.1平衡小车（参考B站草履虫都能学会的平衡小车）

也许不只有平衡小车（doge）

B.1.1硬件部分

直接参考视频（doge）

B.1.2软件部分

晚点再写阿巴阿巴

C结尾

参考文献

CSDN-PID详细教程

哔哩哔哩-草履虫都能学会的平衡小车

留言
有问题请指出,你可以选择以下方式：

在下方评论区留言

邮箱留言

Mouse_blog

嵌入式——PID——学习笔记

A引入